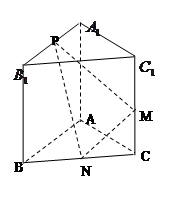如图，已知三棱柱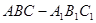
的侧棱与底面垂直，
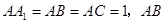⊥AC，M是
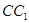的中点，N是BC的中点，点P在直线
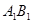上，且满足
.
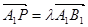（1）当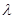
取何值时，直线PN与平面ABC所成的角
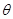最大？
（2）若平面PMN与平面ABC所成的二面角为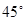
，试确定点P的位置.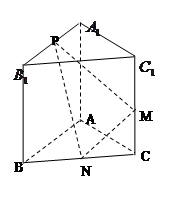
相关试题
的内接△ABC中，点A的坐标是(－3,0)，重心G的坐标是
，求：(1)直线BC的方程;(2)弦BC的
长度.
上截得弦长为2
;③圆心在直线
上，求圆C的方程.
垂直于矩形
所在的平面，
分别是
的中点.
平面
；
平面
.
与直线L2：
的交点M且满足下列条件的
平行；（2
）与直线
中，
，
，四边形
为矩形，平面
平面
.
平面
在线段
上运动，设平面
与平面
所成二面角的平面角为
，试求
的取值范围.
相关知识点
推荐套卷
如图，已知三棱柱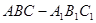的侧棱与底面垂直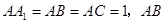，⊥AC，M是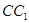的中点，N是BC的中点，点P在直线 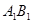上，且满足.
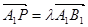（1）当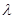取何值时，直线PN与平面ABC所成的角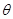最大？
（2）若平面PMN与平面ABC所成的二面角为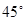，试确定点P的位置.
粤公网安备 44130202000953号