（1）如图①所示，菱形ABCD与等腰△AEF有公共顶点A, AE=AF,∠EAF=∠BAD, 连接BE、DF．
求证：∠ABE =∠ADF．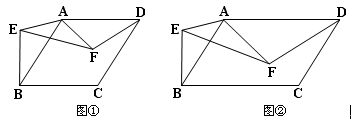
(2) 如图②所示，将（1）中的菱形ABCD变为平行四边形ABCD，等腰△AEF变为一般△AEF，且AD=kAB,AF=kAE,其他条件不变．(1)中的结论是否还成立？说明理由．
相关知识点
推荐套卷
（1）如图①所示，菱形ABCD与等腰△AEF有公共顶点A, AE=AF,∠EAF=∠BAD, 连接BE、DF．
求证：∠ABE =∠ADF．
(2) 如图②所示，将（1）中的菱形ABCD变为平行四边形ABCD，等腰△AEF变为一般△AEF，且AD=kAB,AF=kAE,其他条件不变．(1)中的结论是否还成立？说明理由．
粤公网安备 44130202000953号