已知抛物线C1与x轴的一个交点为交于(-4,0),对称轴为直线x=-1.5,
并过点(-1,6)求抛物线C1的解析式;
求出与抛物线C1关于原点对称的抛物线C2的解析式,并在C1所在的平面直角坐标系中画出C2的图像;
在(2)的条件下,抛物线C1与抛物线C2与相交于A,B两点(点A在点B的左侧).
①求出点A和点B的坐标;
②点P在抛物线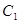 上,且位于点A和点B之间;点Q在抛物线
上,且位于点A和点B之间;点Q在抛物线 上,也位于点A和点B之间.当PQ∥
上,也位于点A和点B之间.当PQ∥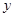 轴时,求PQ长度的最大值.
轴时,求PQ长度的最大值.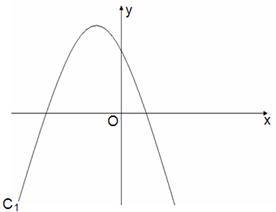
相关知识点
推荐套卷


 ,其中
,其中 .
.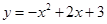 与x轴交于A,B两点,与y轴交于点C,点D为抛物线的顶点,请解决下列问题.
与x轴交于A,B两点,与y轴交于点C,点D为抛物线的顶点,请解决下列问题.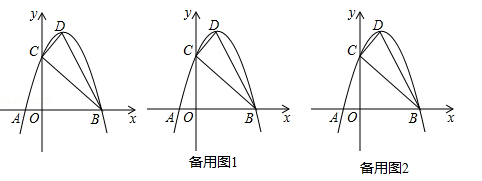
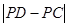 最大时,求a的值并在图中标出点P的位置;
最大时,求a的值并在图中标出点P的位置;
 .tanD=tan15°=
.tanD=tan15°= =
= =
= .
. .假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)=
.假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)= =
= =
= 与双曲线
与双曲线 交于A,B两点,与y轴交于点C,将直线AB绕点C旋转45°后,是否仍与双曲线相交?若能,求出交点P的坐标;若不能,请说明理由.
交于A,B两点,与y轴交于点C,将直线AB绕点C旋转45°后,是否仍与双曲线相交?若能,求出交点P的坐标;若不能,请说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号