某物流公司的甲、乙两辆货车分别从相距300千米的A、B两地同时出发相向而行,并以各自的速度匀速行驶, 1.5小时时甲车先到达配货站C地,此时两车相距30千米,甲车在C地用1小时配货,然后按原速度开往B地;2小时时乙车也到达C地,乙车未停留直接开往A地.乙车的速度是 千米/小时,B、C两地的距离是 千米,A、C两地的距离是 千米;
(2)求甲车的速度及甲车到达B地所用的时间;
(3)乙车出发多长时间,两车相距150千米?
相关知识点
推荐套卷
 中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若
中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若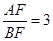 ,求
,求 的值。
的值。
 交BG于点H,则AB和EH的数量关系是,CG和EH的数量关系是,
交BG于点H,则AB和EH的数量关系是,CG和EH的数量关系是, 则
则 的代数式表示),试写出解答过程。
的代数式表示),试写出解答过程。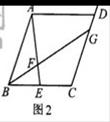
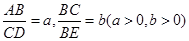 ,则
,则 的值是(用含
的值是(用含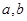 的代数式表示).
的代数式表示).
 ,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?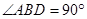 ,请根据以上数据求条幅的长度(结果保留整数.参考数据:
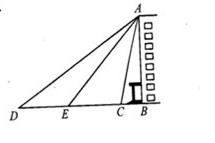
,请根据以上数据求条幅的长度(结果保留整数.参考数据: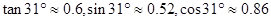 )
)
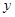 (千米)与
(千米)与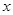 (时间)之间的函数关系图像
(时间)之间的函数关系图像
 ,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号