如图,在平面直角坐标系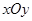 中,半径为1的圆的圆心
中,半径为1的圆的圆心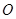 在坐标原点,且与两坐标轴分别交于
在坐标原点,且与两坐标轴分别交于 四点.抛物线
四点.抛物线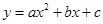 与
与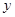 轴交于点
轴交于点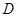 ,与直线
,与直线 交于点
交于点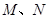 ,且
,且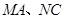 分别与圆
分别与圆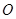 相切于点
相切于点 和点
和点 .
.
求抛物线的解析式;
抛物线的对称轴交
 轴于点
轴于点 ,连结
,连结 ,并延长
,并延长 交圆
交圆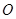 于
于 ,求
,求 的长.
的长.过点
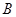 作圆
作圆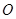 的切线交
的切线交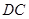 的延长线于点
的延长线于点 ,判断点
,判断点 是否在抛物线上,说明理由.
是否在抛物线上,说明理由.
相关知识点
推荐套卷
如图,在平面直角坐标系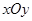 中,半径为1的圆的圆心
中,半径为1的圆的圆心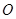 在坐标原点,且与两坐标轴分别交于
在坐标原点,且与两坐标轴分别交于 四点.抛物线
四点.抛物线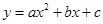 与
与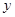 轴交于点
轴交于点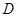 ,与直线
,与直线 交于点
交于点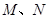 ,且
,且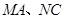 分别与圆
分别与圆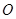 相切于点
相切于点 和点
和点 .
.
求抛物线的解析式;
抛物线的对称轴交
 轴于点
轴于点 ,连结
,连结 ,并延长
,并延长 交圆
交圆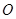 于
于 ,求
,求 的长.
的长.过点
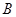 作圆
作圆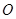 的切线交
的切线交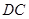 的延长线于点
的延长线于点 ,判断点
,判断点 是否在抛物线上,说明理由.
是否在抛物线上,说明理由.