如图，在△ABO中，已知点
、B（﹣1，﹣1）、C（0，0），正比例函数y=﹣x图象是直线l，直线AC∥x轴交直线l与点C．
（1）C点的坐标为 （﹣3，3） ；
（2）以点O为旋转中心，将△ABO顺时针旋转角α（90°＜α＜180°），使得点B落在直线l上的对应点为B′，点A的对应点为A′，得到△A′OB′．
①∠α= 90° ；②画出△A′OB′．
（3）写出所有满足△DOC∽△AOB的点D的坐标．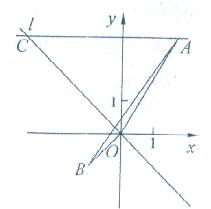
相关试题
，且点B的坐标为（4，2）．画出△OAB绕点O逆时针旋转90
，并求出
的长．
，求
的值．
以3cm／s的速度向D移动，直到D为止，点Q以2cm／s的速度向B移动，点
也随之停止．
？
cm?相关知识点
推荐套卷
粤公网安备 44130202000953号