最近,某人准备将手中的10万块钱投资理财,现有二种方案:第一种方案:将10万块钱全部用来买股票,据分析预测:投资股市一年可能获利40%,也可能亏损20%(只有这两种可能),且获利的概率为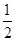 .第二种方案:将10万块钱全部用来买基金,据分析预测:投资基金一年可能获利20%,也可能损失10%,也可能不赔不赚,且三种情况发生的概率分别为
.第二种方案:将10万块钱全部用来买基金,据分析预测:投资基金一年可能获利20%,也可能损失10%,也可能不赔不赚,且三种情况发生的概率分别为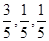 .针对以上两种投资方案,请你为选择一种合理的理财方法,并说明理由.
.针对以上两种投资方案,请你为选择一种合理的理财方法,并说明理由.
相关知识点
推荐套卷
最近,某人准备将手中的10万块钱投资理财,现有二种方案:第一种方案:将10万块钱全部用来买股票,据分析预测:投资股市一年可能获利40%,也可能亏损20%(只有这两种可能),且获利的概率为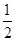 .第二种方案:将10万块钱全部用来买基金,据分析预测:投资基金一年可能获利20%,也可能损失10%,也可能不赔不赚,且三种情况发生的概率分别为
.第二种方案:将10万块钱全部用来买基金,据分析预测:投资基金一年可能获利20%,也可能损失10%,也可能不赔不赚,且三种情况发生的概率分别为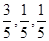 .针对以上两种投资方案,请你为选择一种合理的理财方法,并说明理由.
.针对以上两种投资方案,请你为选择一种合理的理财方法,并说明理由.