已知双曲线 和椭圆
和椭圆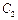 有相同的焦点
有相同的焦点 和
和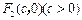 ,两曲线在第一象限内的交点为
,两曲线在第一象限内的交点为 ,椭圆
,椭圆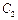 与
与 轴负半轴交于点
轴负半轴交于点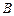 ,且
,且 三点共线,
三点共线, 分有向线段
分有向线段 的比为
的比为 ,又直线
,又直线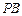 与双曲线
与双曲线 的另一交点为
的另一交点为 ,若
,若 .
.
(1)求椭圆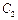 的离心率;
的离心率;
(2)求双曲线 和椭圆
和椭圆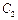 的方程.
的方程.
推荐套卷
已知双曲线 和椭圆
和椭圆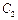 有相同的焦点
有相同的焦点 和
和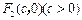 ,两曲线在第一象限内的交点为
,两曲线在第一象限内的交点为 ,椭圆
,椭圆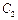 与
与 轴负半轴交于点
轴负半轴交于点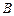 ,且
,且 三点共线,
三点共线, 分有向线段
分有向线段 的比为
的比为 ,又直线
,又直线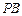 与双曲线
与双曲线 的另一交点为
的另一交点为 ,若
,若 .
.
(1)求椭圆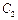 的离心率;
的离心率;
(2)求双曲线 和椭圆
和椭圆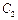 的方程.
的方程.