点A（-1，4）和点B（-5，1）在平面直角坐标系中的位置如图所示．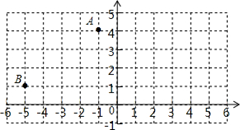
将点A、B分别向右平移5个单位，得到点A1、B1，请画出四边形AA1B1B；
画一条直线，将四边形AA1B1B分成两个全等的图形，并且每个图形都是轴对称图形．
中，x的值为负数，y的值为正数，求m的取值范围.
的整数x的值.
把解集表示在数轴上，并求出不等式组的整数解．
相关知识点
推荐套卷
点A（-1，4）和点B（-5，1）在平面直角坐标系中的位置如图所示．将点A、B分别向右平移5个单位，得到点A1、B1，请画出四边形AA1B1B；
画一条直线，将四边形AA1B1B分成两个全等的图形，并且每个图形都是轴对称图形．
粤公网安备 44130202000953号