2010年11月广州成功举办了第十六届亚运会。在华南理工大学学生会举行的亚运知识有奖问答比赛中，甲、乙、丙同时回答一道有关亚运知识的问题，已知甲回答对这道题目的概率是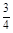
，甲、丙两人都回答错的概率是
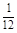，乙、丙两人都回答对的概率是
．
（1）求乙、丙两人各自回答对这道题目的概率．
（2）（理）求回答对这道题目的人数的随机变量
的分布列和期望．
相关试题
，球内接圆锥的高为
，体积为
，
表示
；
，
；
.
内任取两个数（可以相等），分别记为
和
，
，求
的概率.
是定义在
上的减函数，并且满足
，
，
的值， （2）如果
，求x的取值范围。相关知识点
推荐套卷
2010年11月广州成功举办了第十六届亚运会。在华南理工大学学生会举行的亚运知识有奖问答比赛中，甲、乙、丙同时回答一道有关亚运知识的问题，已知甲回答对这道题目的概率是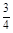，甲、丙两人都回答错的概率是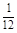，乙、丙两人都回答对的概率是．
（1）求乙、丙两人各自回答对这道题目的概率．
（2）（理）求回答对这道题目的人数的随机变量的分布列和期望．
粤公网安备 44130202000953号