有一种大型商品,A、B两地都有出售,且价格相同,某地居民从两地之一购得商品后运回的费用是:A地每公里的运费是B地每公里运费的3倍. A、B两地距离为10公里,顾客选择A地或B地购买这件商品的标准是:包括运费和价格的总费用较低.已知P地居民选择A地或B地购物总费用相等.
(1)以A、B所在的直线为x轴,线段AB的中点为原点建立如图直角坐标系,试确定点P所在曲线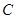 的形状;
的形状;
(2)请说明(1)中曲线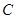 外的居民选择A地购物是否合算?
外的居民选择A地购物是否合算?
相关知识点
推荐套卷
有一种大型商品,A、B两地都有出售,且价格相同,某地居民从两地之一购得商品后运回的费用是:A地每公里的运费是B地每公里运费的3倍. A、B两地距离为10公里,顾客选择A地或B地购买这件商品的标准是:包括运费和价格的总费用较低.已知P地居民选择A地或B地购物总费用相等.
(1)以A、B所在的直线为x轴,线段AB的中点为原点建立如图直角坐标系,试确定点P所在曲线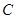 的形状;
的形状;
(2)请说明(1)中曲线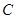 外的居民选择A地购物是否合算?
外的居民选择A地购物是否合算?