如图,矩形OABC的顶点B点坐标为(3,2),点D是BC的中点.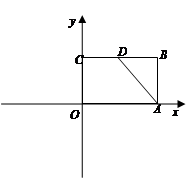
(1)将△ABD向左平移3个单位,则点D的对应点E的坐标为 ;
(2)若点E在双曲线y= 上,则k的值为 ,直线OE与双曲线的另一个交点F的坐标是 ;
上,则k的值为 ,直线OE与双曲线的另一个交点F的坐标是 ;
(3)若在y轴上有一动点P,当点P运动到何处时PB+PF的值最小?求出此时的P点坐标.
相关知识点
推荐套卷
如图,矩形OABC的顶点B点坐标为(3,2),点D是BC的中点.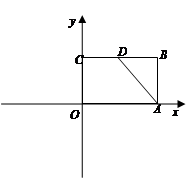
(1)将△ABD向左平移3个单位,则点D的对应点E的坐标为 ;
(2)若点E在双曲线y= 上,则k的值为 ,直线OE与双曲线的另一个交点F的坐标是 ;
上,则k的值为 ,直线OE与双曲线的另一个交点F的坐标是 ;
(3)若在y轴上有一动点P,当点P运动到何处时PB+PF的值最小?求出此时的P点坐标.