生活中,有人喜欢把传送的便条折成 形状,折叠过程是这样的(阴影部分表示纸条的反面):
形状,折叠过程是这样的(阴影部分表示纸条的反面):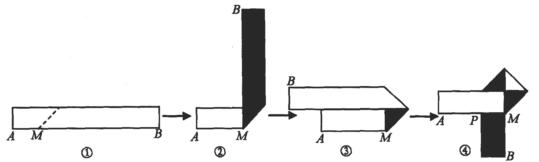
如果由信纸折成的长方形纸条(图①)长为26厘米,回答下列问题:
(1)如果长方形纸条的宽为2厘米,并且开始折叠时起点M与点A的距离为3厘米,那么在图②中,BM=_____厘米;在图④中,BM=_____厘米.
(2)如果不但要折成图④的形状,而且为了美观,希望纸条两端超出点P的长度相等,即最终图形是对称图形,假设长方形纸条的宽为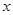 厘米,试求在开始折叠时(图①)起点M与点A的距离(用含
厘米,试求在开始折叠时(图①)起点M与点A的距离(用含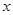 的代数式表示).
的代数式表示).
相关知识点
推荐套卷



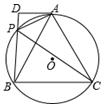
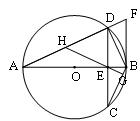
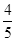 ,DF=9,求⊙O的半径。
,DF=9,求⊙O的半径。 粤公网安备 44130202000953号
粤公网安备 44130202000953号