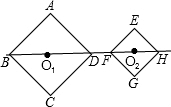
如图,正方形ABCD和正方形EFGH的边长分别为2 2和 2 ,对角线BD、FH都在直线l上.O1、O2分别是正方形的中心,线段O1O2的长叫做两个正方形的中心距.当中心O2在直线l上平移时,正方形EFGH也随之平移,在平移时正方形EFGH的形状、大小没有改变.当中心O2在直线l上平移到两个正方形只有一个公共点时,中心距O1O2等于多少?
随着中心O2在直线l上的平移,两个正方形的公共点的个数还有哪些变化?并求出相对应的中心距的值或取值范围(不必写计算过程).
相关知识点
推荐套卷
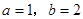
 ;(2)
;(2)
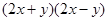 (2)
(2)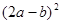
 (4)4-
(4)4- -(2-
-(2-

 与
与 是邻补角,OD、OE分别是
是邻补角,OD、OE分别是
 ,其中a=-2。
,其中a=-2。 粤公网安备 44130202000953号
粤公网安备 44130202000953号