阳光公司生产某种产品,每件成本3元,售价4元,年销售量为20万件,为获得更好的效益,公司准备拿出一定的资金做广告。根据经验,每年投入的广告费是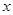 (万元)时,产品的销量是原销量的
(万元)时,产品的销量是原销量的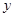 倍,且
倍,且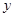 与
与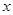 之间满足如果把利润看成是销售总额减去成本费和广告费。
之间满足如果把利润看成是销售总额减去成本费和广告费。试求出年利润
 (万元)与广告费
(万元)与广告费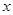 (万元)的函数关系式,并注明
(万元)的函数关系式,并注明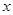 的取值范围;
的取值范围;若
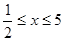 ,要使利润
,要使利润 随广告费
随广告费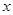 的增大而增大,求
的增大而增大,求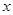 的取值范围。
的取值范围。
相关知识点
推荐套卷
阳光公司生产某种产品,每件成本3元,售价4元,年销售量为20万件,为获得更好的效益,公司准备拿出一定的资金做广告。根据经验,每年投入的广告费是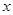 (万元)时,产品的销量是原销量的
(万元)时,产品的销量是原销量的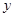 倍,且
倍,且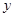 与
与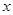 之间满足如果把利润看成是销售总额减去成本费和广告费。
之间满足如果把利润看成是销售总额减去成本费和广告费。试求出年利润
 (万元)与广告费
(万元)与广告费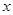 (万元)的函数关系式,并注明
(万元)的函数关系式,并注明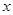 的取值范围;
的取值范围;若
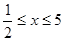 ,要使利润
,要使利润 随广告费
随广告费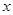 的增大而增大,求
的增大而增大,求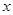 的取值范围。
的取值范围。