如图，是某校的平面示意图，已知图书馆、行政楼的坐标分别为（-3,2），（2,3）.完成以下问题: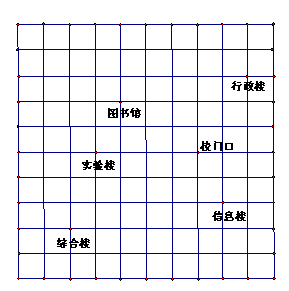
请根据题意在图上建立直角坐标系；
写出图上其他地点的坐标
在图中用点P表示体育馆（-1，-3）的位置
；
；
，
，
，求a、b、c之间有什么样的关系？
，求n的值.
，
，求
的值.相关知识点
推荐套卷
如图，是某校的平面示意图，已知图书馆、行政楼的坐标分别为（-3,2），（2,3）.完成以下问题:请根据题意在图上建立直角坐标系；
写出图上其他地点的坐标
在图中用点P表示体育馆（-1，-3）的位置
粤公网安备 44130202000953号