现有足够多的除颜色外都相同的球供你选用,还有一个最多只能装10个球的不透明袋子.
(1)请你设计一个摸球游戏,使得从袋中任意摸出1个球,摸得红球的概率为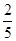 ,则应往袋中如何放球? .
,则应往袋中如何放球? .
(2)若袋中装有2个红球和2个白球,搅匀后从袋中摸出一个球后,不放回,然后再摸出一个球,则请用列表或画树形图的方法列出所有等可能情况,并求出两次摸出的球都是红球的概率.
相关知识点
推荐套卷

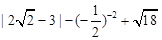 .
.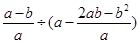 ,其中
,其中 ,
,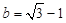 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号