我们知道:有两条边相等的三角形叫做等腰三角形.类似地,我们定义:至少有一组对边相等的四边形叫做等对边四边形.请写出一个你学过的特殊四边形中是等对边四边形的图形的名称;
如图,在
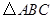 中,点
中,点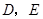 分别在
分别在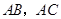 上,设
上,设 相交于点
相交于点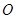 ,若
,若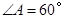 ,
,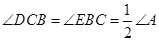 .请你写出图中一个与
.请你写出图中一个与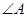 相等的角,并猜想图中哪个四边形是等对边四边形;
相等的角,并猜想图中哪个四边形是等对边四边形;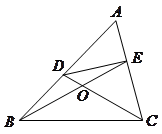
在
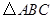 中,如果
中,如果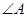 是不等于
是不等于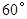 的锐角,点
的锐角,点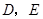 分别在
分别在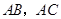 上,且
上,且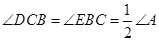 .探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
.探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
相关知识点
推荐套卷
我们知道:有两条边相等的三角形叫做等腰三角形.类似地,我们定义:至少有一组对边相等的四边形叫做等对边四边形.请写出一个你学过的特殊四边形中是等对边四边形的图形的名称;
如图,在
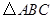 中,点
中,点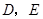 分别在
分别在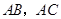 上,设
上,设 相交于点
相交于点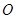 ,若
,若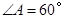 ,
,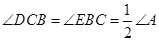 .请你写出图中一个与
.请你写出图中一个与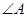 相等的角,并猜想图中哪个四边形是等对边四边形;
相等的角,并猜想图中哪个四边形是等对边四边形;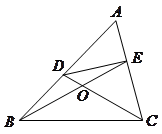
在
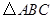 中,如果
中,如果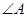 是不等于
是不等于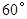 的锐角,点
的锐角,点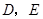 分别在
分别在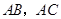 上,且
上,且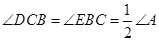 .探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
.探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.