如图,L ,L
,L 分别表示A步行与B骑车在同一路上行驶的路程S(千米)与时间t(小时)的关系。根据图像,回答下列问题:
分别表示A步行与B骑车在同一路上行驶的路程S(千米)与时间t(小时)的关系。根据图像,回答下列问题: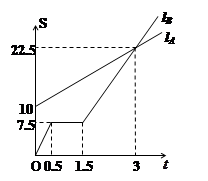
B出发时与A相距 千米。
走了一段路后,自行车发生故障,进行修理,所用的时
间是 小时。B出发后 小时与A相遇
若B的自行车不发生故障,保持出发时的速度前进, 那么与A的相遇点离B的出发点相距 千米。在图中表示出这个相遇点C
相关知识点
推荐套卷
如图,L ,L
,L 分别表示A步行与B骑车在同一路上行驶的路程S(千米)与时间t(小时)的关系。根据图像,回答下列问题:
分别表示A步行与B骑车在同一路上行驶的路程S(千米)与时间t(小时)的关系。根据图像,回答下列问题: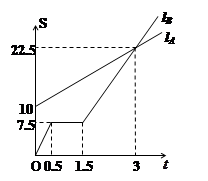
B出发时与A相距 千米。
走了一段路后,自行车发生故障,进行修理,所用的时
间是 小时。B出发后 小时与A相遇
若B的自行车不发生故障,保持出发时的速度前进, 那么与A的相遇点离B的出发点相距 千米。在图中表示出这个相遇点C