如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点为P1(a+6, b+2)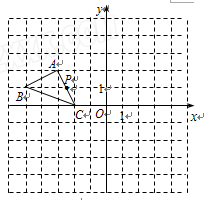
(1)请画出上述平移后的△A1B1C1,并写出点A、C、A1、C1的坐标;
(2)求出以A、C、A1、C1为顶点的四边形的面积.
相关知识点
推荐套卷
如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点为P1(a+6, b+2)
(1)请画出上述平移后的△A1B1C1,并写出点A、C、A1、C1的坐标;
(2)求出以A、C、A1、C1为顶点的四边形的面积.