统计局就某地居民的月收入情况调查了10 000人,并根据所得数据画了样本频率分布直方图,每个分组包括左端点,不包含右端点,如第一组表示收入在 元之间。
元之间。
(1)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这10 000人中用分层抽样方法抽出100人作进一步分析,则月收入在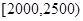 的应抽取多少人;
的应抽取多少人;
(2)根据频率分布直方图估计样本数据的中位数;
(3)根据频率分布直方图估计样本数据的平均数.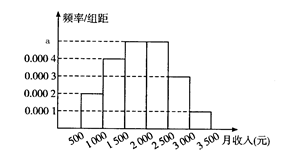
推荐套卷
统计局就某地居民的月收入情况调查了10 000人,并根据所得数据画了样本频率分布直方图,每个分组包括左端点,不包含右端点,如第一组表示收入在 元之间。
元之间。
(1)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这10 000人中用分层抽样方法抽出100人作进一步分析,则月收入在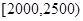 的应抽取多少人;
的应抽取多少人;
(2)根据频率分布直方图估计样本数据的中位数;
(3)根据频率分布直方图估计样本数据的平均数.