甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,甲先从6道备选题中一次性抽取3道题独立作答,然后由乙回答剩余3道题,每人答对其中2题就停止答题,即为闯关成功。已知6道备选题中,甲能答对其中的4道题,乙答对每道题的概率都是 。(Ⅰ)求甲、乙至少有一人闯关成功的概率;
。(Ⅰ)求甲、乙至少有一人闯关成功的概率;
(Ⅱ)设乙答对题目的个数为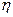 ,求
,求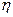 的方差;
的方差; (Ⅲ)设甲答对题目的个数为
(Ⅲ)设甲答对题目的个数为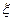 ,求
,求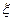 的分布列及数学期望。
的分布列及数学期望。
推荐套卷
甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,甲先从6道备选题中一次性抽取3道题独立作答,然后由乙回答剩余3道题,每人答对其中2题就停止答题,即为闯关成功。已知6道备选题中,甲能答对其中的4道题,乙答对每道题的概率都是 。(Ⅰ)求甲、乙至少有一人闯关成功的概率;
。(Ⅰ)求甲、乙至少有一人闯关成功的概率;
(Ⅱ)设乙答对题目的个数为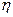 ,求
,求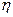 的方差;
的方差; (Ⅲ)设甲答对题目的个数为
(Ⅲ)设甲答对题目的个数为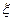 ,求
,求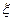 的分布列及数学期望。
的分布列及数学期望。