（本小题满分14分）设函数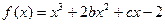
的图象与x轴相交于一点
，且在点处的切线方程是
（I）求t的值及函数
的解析式；
（II）设函数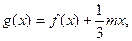
（1）若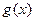
的极值存在，求实数m的取值范围。
（2）假设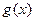有两个极值点
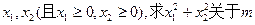的表达式
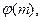并判断
是否有最大值，若有最大值求出它；若没有最大值，说明理由。
相关试题
, x
。
）两点，当x
时恒有
,求实数a的范围。
在x
(2,+∞),恒有
>1，求a的取值范围。
(a>1>b>0),当a,b满足什么关系时，f(x)在(1,+∞)上恒取正值？
+ax+1)。(1)若f(x)的定义域R，求实数a的取值范围；（2）若f(x)的值域为R，求实数a的取值范围。推荐套卷
（本小题满分14分）设函数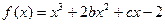的图象与x轴相交于一点，且在点处的切线方程是
（I）求t的值及函数的解析式；
（II）设函数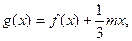
（1）若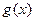的极值存在，求实数m的取值范围。
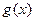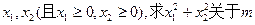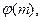（2）假设有两个极值点的表达式并判断是否有最大值，若有最大值求出它；若没有最大值，说明理由。
粤公网安备 44130202000953号