某中学的高二(1)班男同学有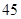
名，女同学有
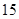名，老师按照分层抽样的方法组建了一个
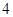人的课外兴趣小组．
（１）求某同学被抽到的概率及课外兴趣小组中男、女同学的人数；
（２）经过一个月的学习、讨论，这个兴趣小组决定选出两名同学做某项实验，方法是先从小组里选出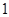
名同学做实验，该同学做完后，再从小组内剩下的同学中选一名同学做实验，求选出的两名同学中恰有一名女同学的概率；
（３）实验结束后，第一次做实验的同学得到的实验数据为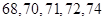
，第二次做实验的同学得到的实验数据为
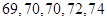，请问哪位同学的实验更稳定？并说明理由.
相关试题
某公司按现有能力，每月收入为70万元，公司分析部门测算，若不进行改革，入世后因竞争加剧收入将逐月减少．分析测算得入世第一个月收入将减少3万元，以后逐月多减少2万元，如果进行改革，即投入技术改造300万元，且入世后每月再投入1万元进行员工培训，则测算得自入世后第一个月起累计收入
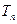与时间n（以月为单位）的关系为=
，且入世第一个月时收入将为90万元，第二个月时累计收入为170万元，问入世后经过几个月，该公司改革后的累计纯收入高于不改革时的累计纯收入．
的解集为空集，求实数k的取值范围.一个袋中有若干个大小相同的黑球、白球和红球。已知从袋中任意摸出1个球，得到黑球的概率是
；从袋中任意摸出2个球，至少得到1个白球的概率是
.
（Ⅰ）若袋中共有10个球，
（i）求白球的个数；
（ii）从袋中任意摸出3个球，记得到白球的个数为
，求随机变量
的数学期望
.
（Ⅱ）求证：从袋中任意摸出2个球，至少得到1个黑球的概率不大于
。并指出袋中哪种颜色的球个数最少.
;
相关知识点
推荐套卷
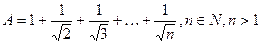
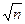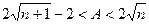
粤公网安备 44130202000953号