已知抛物线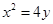
的焦点为
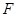，过焦点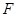且不平行于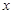
轴的动直线
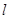交抛物线于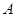
，
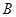两点，抛物线在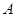、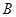两点处的切线交于点
．
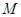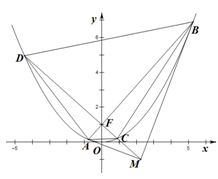
（Ⅰ）求证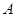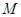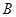：，，三点的横坐标成等差数列；
（Ⅱ）设直线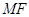
交该抛物线于
，
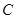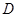两点，求四边形
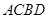面积的最小值．
相关试题
满足
,且
. 
,且{
}为等差数列?若存在,求出t的值;若不存在，说明理由.
中,
,点E是BC上一点,且满足:
,以A为圆心,AC的长为半径作圆交AB于D,交AE于F.若
,求
的值. 
满足:①
;②
. 
的解析式; 
恒成立,求实数m的取值范围.
,
,求实数a的值; 
求实数a的取值范围.
内有一点P(-1,2),AB过点P,若弦长
；
，求直线AB的方程.相关知识点
推荐套卷
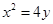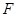已知抛物线的焦点为，过焦点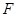且不平行于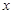轴的动直线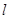交抛物线于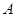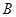，两点，抛物线在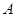、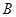两点处的切线交于点．
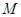（Ⅰ）求证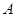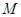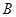：，，三点的横坐标成等差数列；
（Ⅱ）设直线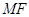交该抛物线于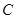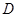，两点，求四边形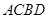面积的最小值．
粤公网安备 44130202000953号