某项试验在甲、乙两地各自独立地试验两次,已知在甲、乙两地每次试验成功的概率依次为 、
、 ;不成功的概率依次为
;不成功的概率依次为 、
、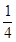 .
.
(Ⅰ)求以上的四次试验中,至少有一次试验成功的概率;
(Ⅱ)在以上的四次试验中,试验成功的次数为 ,求
,求 的分布列,并计算
的分布列,并计算 .
.
推荐套卷
某项试验在甲、乙两地各自独立地试验两次,已知在甲、乙两地每次试验成功的概率依次为 、
、 ;不成功的概率依次为
;不成功的概率依次为 、
、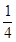 .
.
(Ⅰ)求以上的四次试验中,至少有一次试验成功的概率;
(Ⅱ)在以上的四次试验中,试验成功的次数为 ,求
,求 的分布列,并计算
的分布列,并计算 .
.