如图，矩形ABCD，AB＝6cm，AD＝2cm，点P以2cm/s的速度从顶点A出发沿折线A－B－C向点C运动，同时点Q以lcm/s的速度从顶点C出发向点D运动，当其中一个动点到达末端停止运动时，另一点也停止运动．
(1)问两动点运动几秒，使四边形PBCQ的面积是矩形ABCD面积的
；
(2)问两动点经过多长时间使得点P与点Q之间的距离为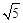
？若存在，求出运动所需的时间；若不存在，请说明理由．
如图，矩形ABCD，AB＝6cm，AD＝2cm，点P以2cm/s的速度从顶点A出发沿折线A－B－C向点C运动，同时点Q以lcm/s的速度从顶点C出发向点D运动，当其中一个动点到达末端停止运动时，另一点也停止运动．
(1)问两动点运动几秒，使四边形PBCQ的面积是矩形ABCD面积的；
(2)问两动点经过多长时间使得点P与点Q之间的距离为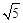？若存在，求出运动所需的时间；若不存在，请说明理由．
与
全等，
与
对应，顶点
与
对应，写出其他对应角及对应顶点．
，
，
，
，
，
，求：
的度数；
的长．
，
与
，
与
是对应点．
．
在同一直线上，且
．求证：
．
，且
，
，
，求
和
的度数．
粤公网安备 44130202000953号