已知A1，A2，B是椭圆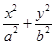
＝1（a>b>0）的顶点（如图），直线l与椭圆交于异于顶点的P，Q两点，且l∥A2B，若椭圆的离心率是
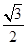，且｜A2B｜＝
。
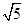（1）求此椭圆的方程；
（2）设直线A1P和直线BQ的倾斜角分别为α，β，试判断α＋β是否为定值？若是，求出此定值；若不是，说明理由。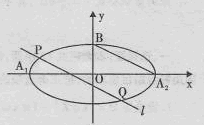
中，
， 
时，
是等比数列，并求
通项公式。
，
，
求：数列
的前n项的和
。
、
、 
。记
，数列
的前n项和
。证明：
的单调性。
，证明：
中，点M、N分别为线段
的中点，平面
侧面
(2)证明：BC
为奇函数，且在
上为增函数， 
， 若
对所有
都成立，求
的取值范围。推荐套卷
已知A1，A2，B是椭圆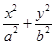＝1（a>b>0）的顶点（如图），直线l与椭圆交于异于顶点的P，Q两点，且l∥A2B，若椭圆的离心率是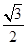，且｜A2B｜＝。
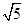（1）求此椭圆的方程；
（2）设直线A1P和直线BQ的倾斜角分别为α，β，试判断α＋β是否为定值？若是，求出此定值；若不是，说明理由。
粤公网安备 44130202000953号