(本小题满分10分)利民商店经销甲、乙两种商品. 现有如下信息:

请根据以上信息,解答下列问题:
(1)甲、乙两种商品的进货单价各多少元?
(2)该商店平均每天卖出甲商品500件和乙商品300件.经调查发现,甲、乙两种商品零售单价分别每降0.1元,这两种商品每天可各多销售100件.为了使每天获取更大的利润,商店决定把甲、乙两种商品的零售单价都下降m元. 在不考虑其他因素的条件下,当m定为多少时,才能使商店每天销售甲、乙两种商品获取的利润之和最大?每天的最大利润是多少?
相关知识点
推荐套卷
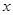 的一元二次方程
的一元二次方程 有两个实数根
有两个实数根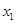 和
和 .
. 的取值范围;
的取值范围; 时,求
时,求

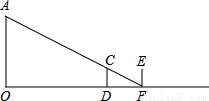
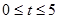 时△BPQ的面积S( cm2)与点P的运动时间t(s)的函数图象.
时△BPQ的面积S( cm2)与点P的运动时间t(s)的函数图象.
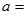 ;
; 粤公网安备 44130202000953号
粤公网安备 44130202000953号