“校园手机”现象越来越受到社会的关注﹒春节期间，小明随机调查了城区若干名同学和家长对中学生带手机现象的看法．统计整理并制作了如下的统计图：
这次的调查对象中，家长有 ▲ 人；
图②中表示家长“赞成”的圆心角的度数为 ▲ 度；
开学后，甲、乙两所学校对各自学校所有学生带手机情况进行了统计，发现两校共有384名学生带手机，且乙学校带手机的学生数是甲学校带手机学生数的，求甲、乙两校中带手机的学生数各有多少？
（本小题满分5分）已知：如图，在△ABC中，
∠ACB=90°点D是AB的中点，延
长BC到点F，
延长CB到点E，使CF=BE，联结DE、DC、DF．
求证：DE=DF．
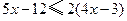，并把它的解集在数轴上表示出来．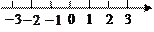
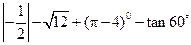．如图1，在平面直角坐标系中，等腰直角三角形OMN的斜边ON在x轴上，顶点M的坐标为（3，3），MH为斜边上的高．抛物线C：
与直线
及
过N点垂直于x轴的直线交于点D．点P（m，0）是x轴上一动点，过点P作y轴的平行线，交射线OM与点E．设以M、E、H、N为顶点的四边形的面积为S．
（1）直接写出点D的坐标及n的值；
（2）判断抛物线C的顶点是否在直线OM上？并说明理由；
（3）当m≠3时，求S与m的函数关系式；
（4）如图2，设直线PE交射线OD于R，交抛物线C于点Q，
以RQ为一边，在RQ的右侧作矩形RQFG，其中RG=
，
直接写出矩形RQFG与等腰直角三角形OMN重叠部分为
轴对称图形时m的取值范围．
现场学习：我们知道，若锐角α的三角函数值为sinα= m，则可通过计算器得到角α的大小，这时我们用arc sin m来表示α，记作：α="arc" sin m；若cos α = m，则记α=" arc" cos m；若tan α= m，则记α=" arc" tan m．
解决问题：如图，已知正方形ABCD，点E是边AB上一动点，点F在AB边或其延长线上，点G在边AD上．连结ED，FG，交点为H．
（1）如图1，若AE=BF=GD，请直接写出∠EHF=°；
（2）如图2，若EF=
CD，GD=AE，设∠EHF=α．请判断当点E在AB上运动时， ∠EHF的大小是否发生变化？若发生变化，请说明理由；若不发生变化，请求出α．
粤公网安备 44130202000953号