已知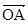
＝(2asin2x，a)，
＝(－1,2
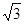sinxcosx＋1)，O为坐标原点，a≠0，设f(x)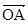＝·＋b，b>a。
(1)若a>0，写出函数y＝f(x)的单调递增区间；
(2)若函数y＝f(x)的定义域为[
，π]，值域为[2,5]，求实数a与b的值。
的前
项和为
， 
，且
，
，
成等差数列.
通项公式；
，求数列
前
．
求证：
。
，VC=7，画出二面角V-AB-C的平面角，并求它的余弦值。
，三条直线a,b,c共点，知：
且
。求证: 
中,求直线
与平面
所成的角。相关知识点
推荐套卷
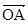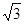已知＝(2asin2x，a)，＝(－1,2sinxcosx＋1)，O为坐标原点，a≠0，设f(x)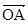＝·＋b，b>a。
(1)若a>0，写出函数y＝f(x)的单调递增区间；
(2)若函数y＝f(x)的定义域为[，π]，值域为[2,5]，求实数a与b的值。
粤公网安备 44130202000953号