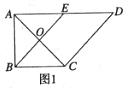
【2015高考陕西,理18】(本小题满分12分)如图 ,在直角梯形
,在直角梯形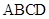 中,
中,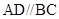 ,
,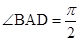 ,
,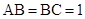 ,
, ,
,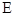 是
是 的中点,
的中点,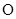 是
是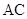 与
与 的交点.将
的交点.将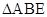 沿
沿 折起到
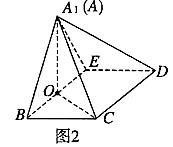
折起到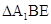 的位置,如图
的位置,如图 .
.
(Ⅰ)证明: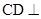 平面
平面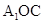 ;
;
(Ⅱ)若平面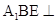 平面
平面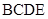 ,求平面
,求平面 与平面
与平面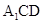 夹角的余弦值.
夹角的余弦值.
推荐套卷
【2015高考陕西,理18】(本小题满分12分)如图 ,在直角梯形
,在直角梯形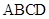 中,
中,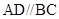 ,
,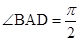 ,
,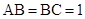 ,
, ,
,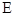 是
是 的中点,
的中点,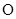 是
是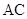 与
与 的交点.将
的交点.将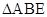 沿
沿 折起到
折起到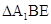 的位置,如图
的位置,如图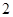 .
.


(Ⅰ)证明: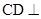 平面
平面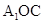 ;
;
(Ⅱ)若平面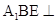 平面
平面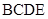 ,求平面
,求平面 与平面
与平面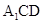 夹角的余弦值.
夹角的余弦值.