(本大题10分)一司机驾驶汽车从甲地去乙地,以80千米/小时的平均速度用6小时到达目的地.(1)当他按原路匀速返回时,求汽车速度v(千米/小时)与时间t(小时)之间的函数关系式;(2)如果该司机匀速返回时,用了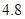 小时,求返回时的速度.
小时,求返回时的速度.
相关知识点
推荐套卷
(本大题10分)一司机驾驶汽车从甲地去乙地,以80千米/小时的平均速度用6小时到达目的地.(1)当他按原路匀速返回时,求汽车速度v(千米/小时)与时间t(小时)之间的函数关系式;(2)如果该司机匀速返回时,用了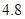 小时,求返回时的速度.
小时,求返回时的速度.