一辆汽车从A地驶往B地，前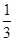
路段为普通公路，其余路段为高速公路．已知汽车在普通公路上行驶的速度为60km/h，在高速公路上行驶的速度为100km/h，汽车从A地到B地一共行驶了2.2h．
请你根据以上信息，就该汽车行驶的“路程”或“时间”，提出一个用二元一次方程组解决的问题，并写出解答过程．
相关试题
，其中，
.
－(－4)
+
－2cos30°
的正整数解。
轴于点C，A
，B
．动点P从O点出发，沿
轴正方向以每秒1个单位长度的速度移动．过P点作PQ垂直于直线OA，垂足为Q．设
点移动的时间为秒，△OPQ与直角梯形OABC重叠部分的面积为S．
相关知识点
推荐套卷
一辆汽车从A地驶往B地，前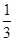路段为普通公路，其余路段为高速公路．已知汽车在普通公路上行驶的速度为60km/h，在高速公路上行驶的速度为100km/h，汽车从A地到B地一共行驶了2.2h．
请你根据以上信息，就该汽车行驶的“路程”或“时间”，提出一个用二元一次方程组解决的问题，并写出解答过程．
粤公网安备 44130202000953号