(本题满分12分) 某工厂有一种材科,可加工甲、乙、丙三种型号机械配件共240个.厂方计划由20个工人一天内加工完成.并要求每人只加工一种配件.根据下表提供的信息。解答下列问题:
(1)设加工甲种配件的人数为x,加工乙种配件的人数为y,求y与x之间的函数关系式。
(2)如果加工每种配件的人数均不少于3人.那么加工配件的人数安排方案有几种?写出每种安排方案.
(3)要使此次加工配件的利润最大,应采用(2)中哪种方案?并求出最大利润值.
相关知识点
推荐套卷
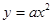 的图象经过点(2,1)。
的图象经过点(2,1)。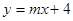 的图象与二次函数
的图象与二次函数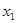 ,
,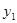 ),B(
),B(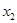 ,
,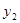 )两点
)两点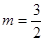 时(图①),求证:△AOB为直角三角形;
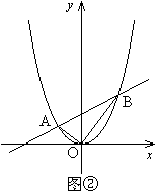
时(图①),求证:△AOB为直角三角形; 时(图②),△AOB的形状,并证明;
时(图②),△AOB的形状,并证明;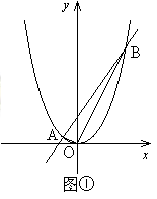
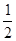 ),B(-1,2)是一次函数
),B(-1,2)是一次函数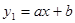 与反比例函数
与反比例函数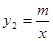 图象的两个交点, AC⊥
图象的两个交点, AC⊥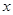 轴于点C,BD⊥
轴于点C,BD⊥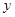 轴于点D。
轴于点D。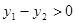 ?
?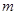 的值;
的值;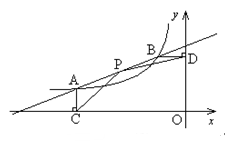
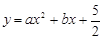 与直线AB交于点A(-1,0),B(4,
与直线AB交于点A(-1,0),B(4,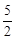 ).点D是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线CD与y轴平行,交直线
).点D是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线CD与y轴平行,交直线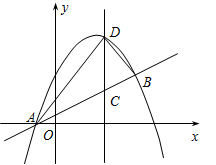
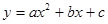 经过点D(-1,0),D(0,-1),E(1,0).
经过点D(-1,0),D(0,-1),E(1,0).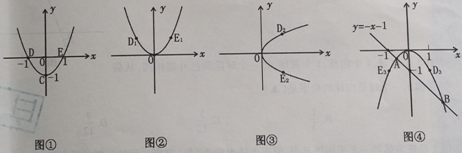
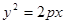 ,点D1与D2是旋转前后的对应点,求图③中抛物线的函数表达式.
,点D1与D2是旋转前后的对应点,求图③中抛物线的函数表达式.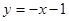 相交于A、B两点,D2与D3是旋转前后如图④,求线段AB的长.
相交于A、B两点,D2与D3是旋转前后如图④,求线段AB的长.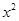 +(2m-1)x+
+(2m-1)x+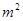 -1经过坐标原点,且当x<0时,y随x的增大而减小.
-1经过坐标原点,且当x<0时,y随x的增大而减小. 粤公网安备 44130202000953号
粤公网安备 44130202000953号