（贵州省安顺市）（本题14分）
如图，抛物线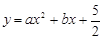
与直线AB交于点A（-1，0），B（4，
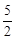）．点D是抛物线A，B两点间部分上的一个动点（不与点A，B重合），直线CD与y轴平行，交直线
AB于点C，连接AD，BD．
（1）求抛物线的解析式；
（2）设点D的横坐标为m，△ADB的面积为S，求S关于m 的函数关系式，并求出当S 取最大值时的点C的坐标；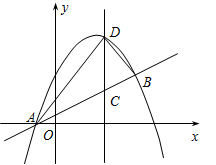
（贵州省安顺市）（本题14分）
如图，抛物线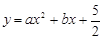与直线AB交于点A（-1，0），B（4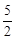，）．点D是抛物线A，B两点间部分上的一个动点（不与点A，B重合），直线CD与y轴平行，交直线
AB于点C，连接AD，BD．
（1）求抛物线的解析式；
（2）设点D的横坐标为m，△ADB的面积为S，求S关于m 的函数关系式，并求出当S 取最大值时的点C的坐标；
．
．
．
；
，并将其解集表示在数轴上．
．
粤公网安备 44130202000953号