某射击小组有甲、乙两名射手，甲的命中率为
，乙的命中率为
，在射击比武活动中每人射击两发子弹则完成一次检测，在一次检测中，若两人命中次数相等且都不少于一发，则称该射击小组为“先进和谐组”.（Ⅰ）若
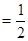，求该小组在一次检测中荣获“先进和谐组”的概率；（Ⅱ）计划在2011年每月进行1次检测，设这12次检测中该小组获得“先进和谐组”的次数为
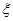， 如果
，求的取值范围．
相关试题
，
，求方程
的根；
满足
，求函数在
的值域；
满足
．
为何值时，复数
对应点在第一象限．
.
为R上的减函数;
.
（厘米）满足关系式：
，若无隔热层，则每年能源消耗费用为8万元.设
为隔热层建造费用与使用20年的能源消耗费用之和.推荐套卷
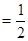某射击小组有甲、乙两名射手，甲的命中率为，乙的命中率为，在射击比武活动中每人射击两发子弹则完成一次检测，在一次检测中，若两人命中次数相等且都不少于一发，则称该射击小组为“先进和谐组”.（Ⅰ）若，求该小组在一次检测中荣获“先进和谐组”的概率；（Ⅱ）计划在2011年每月进行1次检测，设这12次检测中该小组获得“先进和谐组”的次数为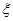， 如果，求的取值范围．
粤公网安备 44130202000953号