某单位为了参加上级组织的普及消防知识竞赛，需要从两名选手中选出一人参加．为此，设计了一个挑选方案：选手从6道备选题中一次性随机抽取3题．通过考察得知：6道备选题中选手甲有4道题能够答对，2道题答错；选手乙答对每题的概率都是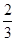
，且各题答对与否互不影响．设选手甲、选手乙答对的题数分别为ξ，η.
(1)写出ξ的概率分布列，并求出E(ξ)，E(η)；
(2)求D(ξ)，D(η)．请你根据得到的数据，建议该单位派哪个选手参加竞赛？
相关试题
，
，
，
，
；
.
，
，
，向量
与
夹角为
，
及
；（2）求与向量
量
的坐标；
，
为第二象限角，求
和
及
的值.
处取得极值。
的单调区间；
在区间（0，2）有两个不等实根，求实数b的取值范围。推荐套卷
某单位为了参加上级组织的普及消防知识竞赛，需要从两名选手中选出一人参加．为此，设计了一个挑选方案：选手从6道备选题中一次性随机抽取3题．通过考察得知：6道备选题中选手甲有4道题能够答对，2道题答错；选手乙答对每题的概率都是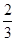，且各题答对与否互不影响．设选手甲、选手乙答对的题数分别为ξ，η.
(1)写出ξ的概率分布列，并求出E(ξ)，E(η)；
(2)求D(ξ)，D(η)．请你根据得到的数据，建议该单位派哪个选手参加竞赛？
粤公网安备 44130202000953号