已知函数 ,其中常数a>0.
,其中常数a>0.
(I )当a>2时,求函数f(x)的单调递增区间;
(II)当a=4时,给出两类直线: 与
与 ,其中m,n为常数.判断这两类直线中是否存在
,其中m,n为常数.判断这两类直线中是否存在 的切线?若存在,求出相应的m或n的值;若不存在,说明理由;
的切线?若存在,求出相应的m或n的值;若不存在,说明理由;
(III)设定义在D上的函数 在点
在点 处的切线方程为
处的切线方程为 ,当
,当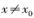 时,若
时,若 在D内恒成立,则称P为函数
在D内恒成立,则称P为函数 的“类对称点”.当a=4时,试问
的“类对称点”.当a=4时,试问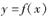 是否存在“类对称点”?若存在,请至少求出一个“类对称点”的横坐标;若不存在,说明理由.
是否存在“类对称点”?若存在,请至少求出一个“类对称点”的横坐标;若不存在,说明理由.
推荐套卷
已知函数 ,其中常数a>0.
,其中常数a>0.
(I )当a>2时,求函数f(x)的单调递增区间;
(II)当a=4时,给出两类直线: 与
与 ,其中m,n为常数.判断这两类直线中是否存在
,其中m,n为常数.判断这两类直线中是否存在 的切线?若存在,求出相应的m或n的值;若不存在,说明理由;
的切线?若存在,求出相应的m或n的值;若不存在,说明理由;
(III)设定义在D上的函数 在点
在点 处的切线方程为
处的切线方程为 ,当
,当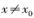 时,若
时,若 在D内恒成立,则称P为函数
在D内恒成立,则称P为函数 的“类对称点”.当a=4时,试问
的“类对称点”.当a=4时,试问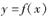 是否存在“类对称点”?若存在,请至少求出一个“类对称点”的横坐标;若不存在,说明理由.
是否存在“类对称点”?若存在,请至少求出一个“类对称点”的横坐标;若不存在,说明理由.