(本小题满分12分)张师傅驾车从公司开往火车站,途径4个交通岗,这4个交通岗将公司到火车站分成5个时段,每个时段的驾车时间都是3分钟,如果遇到红灯要停留1分钟。假设他在各交通岗遇到红灯是相互独立的,并且概率都是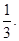
(1)求张师傅此行程时间不小于16分钟的概率;
(2)记张师傅此行程所需时间为Y分钟,求Y的分布列和均值。
相关知识点
推荐套卷
(本小题满分12分)张师傅驾车从公司开往火车站,途径4个交通岗,这4个交通岗将公司到火车站分成5个时段,每个时段的驾车时间都是3分钟,如果遇到红灯要停留1分钟。假设他在各交通岗遇到红灯是相互独立的,并且概率都是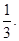
(1)求张师傅此行程时间不小于16分钟的概率;
(2)记张师傅此行程所需时间为Y分钟,求Y的分布列和均值。