(本小题满分15分).
已知 、
、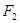 分别为椭圆
分别为椭圆 :
: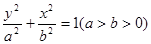 的
的
上、下焦点,其中 也是抛物线
也是抛物线 :
: 的焦点,
的焦点,
点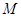 是
是 与
与 在第二象限的交点,且
在第二象限的交点,且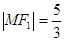 。
。
(Ⅰ)求椭圆的方程;
(Ⅱ)已知点P(1,3)和圆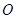 :
: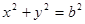 ,过点P的动直线
,过点P的动直线 与圆
与圆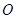 相交于不同的两点A,B,在线段AB取一点Q,满足:
相交于不同的两点A,B,在线段AB取一点Q,满足: ,
,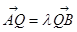 (
(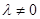 且
且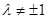 )。求证:点Q总在某定直线上。
)。求证:点Q总在某定直线上。
推荐套卷
(本小题满分15分).
已知 、
、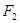 分别为椭圆
分别为椭圆 :
: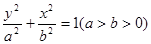 的
的
上、下焦点,其中 也是抛物线
也是抛物线 :
: 的焦点,
的焦点,
点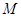 是
是 与
与 在第二象限的交点,且
在第二象限的交点,且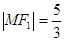 。
。
(Ⅰ)求椭圆的方程;
(Ⅱ)已知点P(1,3)和圆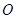 :
: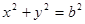 ,过点P的动直线
,过点P的动直线 与圆
与圆 相交于不同的两点A,B,在线段AB取一点Q,满足:
相交于不同的两点A,B,在线段AB取一点Q,满足: ,
,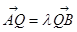 (
(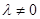 且
且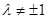 )。求证:点Q总在某定直线上。
)。求证:点Q总在某定直线上。