（本小题满分14分）
已知各项均为正数的数列{an}前n项和为Sn，(p – 1)Sn = p2 – an，n ∈N*，p > 0且p≠1，数列{bn}满足bn = 2logpan．
（Ⅰ）若p =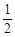
，设数列
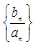的前n项和为Tn，求证：0 < Tn≤4；
（Ⅱ）是否存在自然数M，使得当n > M时，an > 1恒成立？若存在，求出相应的M；若不存在，请说明理由．
相关试题
中，D是BC的中点，
；（Ⅱ）求证：
；（Ⅲ）求三棱锥
的体积.
.（Ⅰ）求
函数图象的对称轴方程；（Ⅱ）求
时,求函数
的最大值,最小值.
中，
，
.（Ⅰ）求角
；（Ⅱ）设
，求
，
，函数
的图象在点
处的切线平行于
轴．
与
的关系；
，都有
成立．
为常数，数列
满足：
，
，
．
时，求数列
有：
；
，且对
，证明：
．推荐套卷
（本小题满分14分）
已知各项均为正数的数列{an}前n项和为Sn，(p – 1)Sn = p2 – an，n ∈N*，p > 0且p≠1，数列{bn}满足bn = 2logpan．
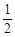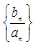（Ⅰ）若p =，设数列的前n项和为Tn，求证：0 < Tn≤4；
（Ⅱ）是否存在自然数M，使得当n > M时，an > 1恒成立？若存在，求出相应的M；若不存在，请说明理由．
粤公网安备 44130202000953号