(本小题满分12分)
某高中社团进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次是否开通“微博”的调查,若开通“微博”的称为“时尚族”,否则称为“非时尚族”。通过调查分别得到如图1所示统计表如图2所示各年龄段人数频率分布直方图: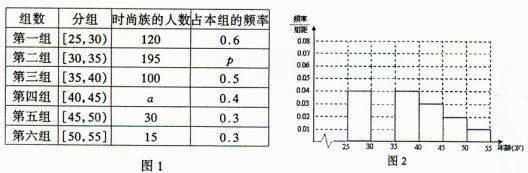
请完成下列问题:
(1)补全频率分布直方图,并求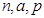 的值;
的值;
(2)从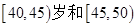 岁年龄段的“时尚族”中采用分层抽样法抽取18人参加网络时尚达人大赛,其中选取3人作为领队,求选取的3名领队年龄在
岁年龄段的“时尚族”中采用分层抽样法抽取18人参加网络时尚达人大赛,其中选取3人作为领队,求选取的3名领队年龄在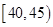 岁的人数为X,求X的分布列和期望E(X)。
岁的人数为X,求X的分布列和期望E(X)。
相关知识点
推荐套卷
 与四边形
与四边形 都是梯形,
都是梯形, ,
,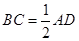 ,
, ,
, ,
, 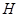 是
是 的中点.
的中点.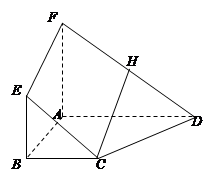
 平面
平面 、
、 、
、 、
、 四点是否共面,并说明理由.
四点是否共面,并说明理由.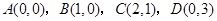 ,将四边形
,将四边形 绕
绕 轴旋转一周,求所得旋转体的表面积和体积.
轴旋转一周,求所得旋转体的表面积和体积.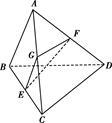
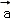 =(
=(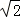 cosωx,1),
cosωx,1),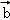 =(2sin(ωx+
=(2sin(ωx+ ),﹣1)(其中
),﹣1)(其中 ≤ω≤
≤ω≤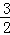 ),
),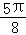 .
.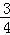 π)的值;
π)的值; )=
)= ,f(
,f(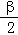 ﹣
﹣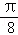 )=
)= ,且
,且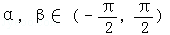 ,
, 粤公网安备 44130202000953号
粤公网安备 44130202000953号