（普通班）设函数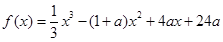
，其中常数
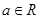；（1）讨论
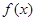的单调性；（2）若
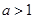，当
，
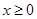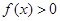恒成立，求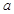
的取值范围。
（实验班）已知椭圆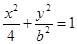
（0＜b＜2）的离心率等于
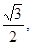抛物线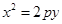
（p＞0）.
（1）若抛物线的焦点F在椭圆的顶点上，求椭圆和抛物线的方程；
（2）若抛物线的焦点F为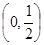
，在抛物线上是否存在点P，使得过点P的切线与椭圆相交于A，B两点，且满足
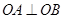？若存在，求出点P的坐标；若不存在，请说明理由.
，判断它的奇偶性。
，
的图像；（2）解不等式
。
是定义在
上的减函数，并且满足
，
，
的值， （2）如果
，求x的取值范围。
是定义在R上的函数，
，
。
.
上画出函数
的图像；
时，求证：在区间
上，
的图像位于函数
推荐套卷
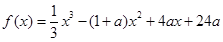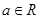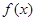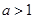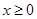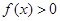（普通班）设函数，其中常数；（1）讨论的单调性；（2）若，当，恒成立，求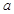的取值范围。
（实验班）已知椭圆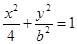（0＜b＜2）的离心率等于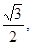抛物线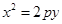（p＞0）.
（1）若抛物线的焦点F在椭圆的顶点上，求椭圆和抛物线的方程；
（2）若抛物线的焦点F为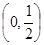，在抛物线上是否存在点P，使得过点P的切线与椭圆相交于A，B两点，且满足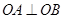？若存在，求出点P的坐标；若不存在，请说明理由.
粤公网安备 44130202000953号