．(本小题满分l 4分)
如图，在边长为4的菱形ABCD中，∠DAB=60°．点E、F分别在边CD、CB上，点E与点C、D不重合，EF⊥AC，EF∩AC=O．沿EF将△CEF翻折到△PEF的位置，使平面PEF⊥平面ABFED．
(Ⅰ)求证：BD⊥平面POA；
(Ⅱ)当PB取得最小值时，请解答以下问题：
(i)求四棱锥P-BDEF的体积；
(ii)若点Q满足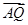
=λ
(λ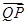 >0)，试探究：直线OQ与平面PBD所成角的大小是否一定大于
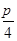?并说明理由．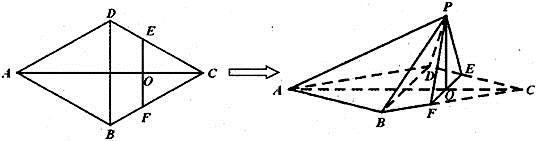
．
在
上恒成立，求m取值范围；
（
）． 
）
.
在
上单调递增，求实数
的取值范围.
，若
的最小值是
，求函数
，且
图象的相邻两条对称轴间的距离为
，
的值；
上的值域.
中，内角
对边分别为
，
的值.
的值；
，求
的值.推荐套卷
．(本小题满分l 4分)
如图，在边长为4的菱形ABCD中，∠DAB=60°．点E、F分别在边CD、CB上，点E与点C、D不重合，EF⊥AC，EF∩AC=O．沿EF将△CEF翻折到△PEF的位置，使平面PEF⊥平面ABFED．
(Ⅰ)求证：BD⊥平面POA；
(Ⅱ)当PB取得最小值时，请解答以下问题：
(i)求四棱锥P-BDEF的体积；
(ii)若点Q满足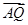=λ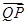 (λ >0)，试探究：直线OQ与平面PBD所成角的大小是否一定大于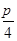?并说明理由．
粤公网安备 44130202000953号