袋中装有13个红球和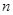 个白球,这些红球和白球除了颜色不同之外,其余都相同,从袋中同时取两个球.
个白球,这些红球和白球除了颜色不同之外,其余都相同,从袋中同时取两个球.
(1)若取出的是2个红球的概率等于取出的是一红一白两个球的概率的3倍,试求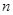 的值;
的值;
(2) 某公司的某部门有21位职员,公司将进行抽奖活动,在(1)的条件下,规定:每个职员都从袋中同时取两个球,然后放回袋中,摇匀再给别人抽奖,若某人取出的两个球是一红一白时,则中奖(奖金1000元);否则,不中奖(也发鼓励奖金100元).试求此公司在这次抽奖活动中所发奖金总额的期望值.
相关知识点
推荐套卷
 若f(-1)=0,且对任意实数x均有f(x)≥0成立.
若f(-1)=0,且对任意实数x均有f(x)≥0成立.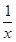 (a为常数).
(a为常数). 粤公网安备 44130202000953号
粤公网安备 44130202000953号