已知圆C过点（1,0）,且圆心在x轴的正半轴上，直线l:y=x-1被圆C所截得的弦长为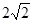
.
(1)求过圆心且与直线l垂直的直线m方程;
(2)点P在直线m上，求以A（-1，0），B（1，0）为焦点且过P点的长轴长最小的椭圆的方程.
，求作向量
=
, 
= 
,试用
, 
, 
，
。
；（2）（
－
）－（
－
）。
=
，
=
、
及向量
的坐标；
．
的顶点
、
、
，求顶点
的标．推荐套卷
已知圆C过点（1,0）,且圆心在x轴的正半轴上，直线l:y=x-1被圆C所截得的弦长为.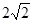
(1)求过圆心且与直线l垂直的直线m方程;
(2)点P在直线m上，求以A（-1，0），B（1，0）为焦点且过P点的长轴长最小的椭圆的方程.
粤公网安备 44130202000953号