将全体正整数组成的数列1,2,3,···,n,······进行如下的分组:(1),(2,3),(4,5,6),······.即第n组含有n个正整数(n="1,2,3," ·····),记第n组各数的和为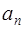 .
.
(Ⅰ)、求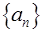 的通项
的通项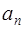 ;
;
(Ⅱ)、求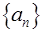 的前n项和
的前n项和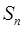 .
.
推荐套卷
将全体正整数组成的数列1,2,3,···,n,······进行如下的分组:(1),(2,3),(4,5,6),······.即第n组含有n个正整数(n="1,2,3," ·····),记第n组各数的和为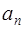 .
.
(Ⅰ)、求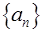 的通项
的通项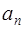 ;
;
(Ⅱ)、求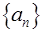 的前n项和
的前n项和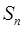 .
.