设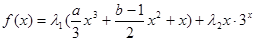
．
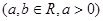(1)当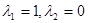
，设x1，x2是f(x)的两个极值点，且满足x1<1<x2<2，求证：
；
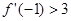(2)当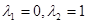
时，
①求函数
(x>0)的最小值；
②对于任意正实数a,b,c，当a+b+c=3时，求证：3aa+3bb+3cc≥9
相关试题
的取值范围.
、
是两个不共线的向量，若它们起点相同，
、
+
+
+
=4
推荐套卷
设 ．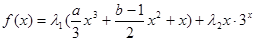
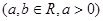(1)当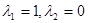，设x1，x2是f(x)的两个极值点，且满足x1<1<x2<2，求证：；
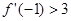(2)当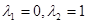时，
①求函数 (x>0)的最小值；
②对于任意正实数a,b,c，当a+b+c=3时，求证：3aa+3bb+3cc≥9
粤公网安备 44130202000953号