如图，四棱锥S-ABCD的底面是正方形，每条侧棱的长都是底面边长的
倍，P为侧棱SD上的点.
（1）求证：AC⊥SD；
（2）若SD⊥平面PAC，求二面角P-AC-D的大小
（3）在（2）的条件下，侧棱SC上是否存在一点E，使得BE∥平面PAC.若存在，求SE：EC的值；若不存在，试说明理由.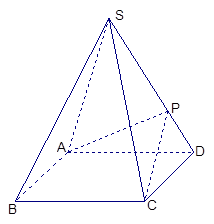
相关试题
，直线
所围成的图形的面积
示选手的最后成绩（各评委所给有效分数的平均值）那么图中①②处分别为，。“S1=S-max-min”的含义
推荐套卷
如图，四棱锥S-ABCD的底面是正方形，每条侧棱的长都是底面边长的倍，P为侧棱SD上的点.
（1）求证：AC⊥SD；
（2）若SD⊥平面PAC，求二面角P-AC-D的大小
（3）在（2）的条件下，侧棱SC上是否存在一点E，使得BE∥平面PAC.若存在，求SE：EC的值；若不存在，试说明理由.
粤公网安备 44130202000953号